周刊(第21期):Lamport时钟介绍
引言:在分布式系统中,由于有多个机器(进程)在一起协调工作,于是如何定义分布式系统中事件的先后顺序就成了难题,本文介绍论文 《Time, Clocks, and the Ordering of Events in a Distributed System》中提到的Lamport时钟。
Lamport时钟介绍
概论
在分布式系统中,由于有多个机器(进程)在一起协调工作,于是如何定义分布式系统中事件的先后顺序就成了难题,本文介绍论文 《Time, Clocks, and the Ordering of Events in a Distributed System》中提到的Lamport时钟。
内容以如下的顺序展开:
- 物理时钟的问题在哪里?(解决了什么问题)
- 全序和偏序关系。(数学基础)
- Lamport时钟的原理介绍、
happen-before关系介绍。(原理介绍) - 分布式一致性的基础。(更远的影响)
物理时钟的问题
分布式系统中定义一个事件的先后顺序是一个难点,下意识的第一反应是:给每个事件加上一个物理的时间戳,不就可以比较不同事件的时间戳来决定其顺序了吗?
这样做的问题在于:在分布式系统中,由多个机器组合起来协调工作,而每个机器上的物理时间也不尽相同,所以“物理时间戳”本质上是一个机器属性,并不一定系统中所有机器都满足同一个时间度量。
以下图为例:
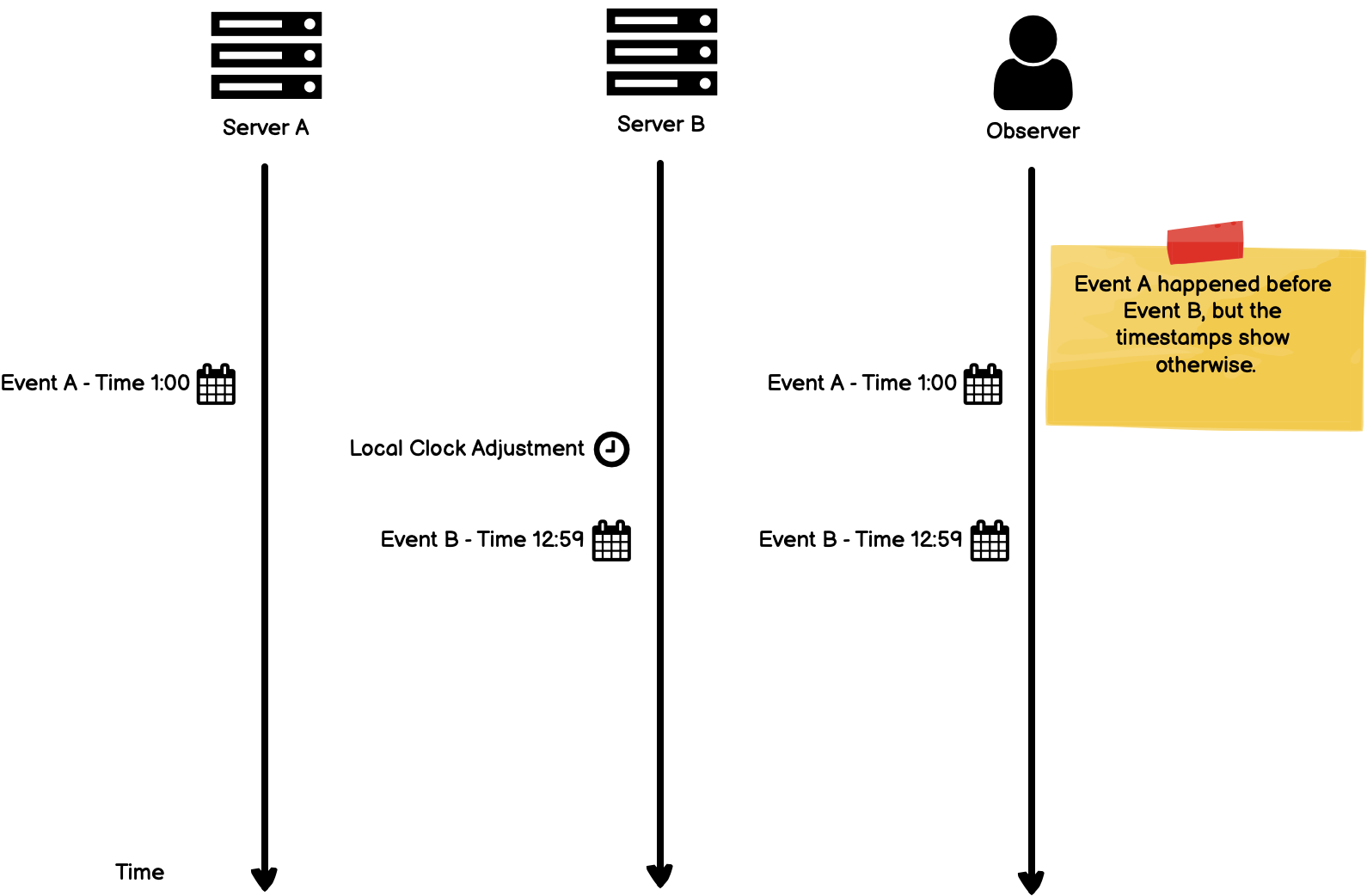
(引用自Lamport Clocks - Kevin Sookocheff)
上图中:
- server A在发出事件A时,打上了本机的时间戳1点。
- 同理,server B给事件B打上了本机的时间戳12:59。
- 可以看到这两个事件都以本地时间为准,当观察者进程收到这两个事件的时候,先后顺序与事件上所带的时间戳并不一致:先收到了时间戳更大的事件A。
这个例子说明:在分布式系统中,以“物理时间”来衡量事件的先后顺序,并不可行。
全序和偏序
在继续讲解之前,还需要了解两个数学上的概念:全序(total ordering)和偏序(partial ordering)关系。
我们首先来定义集合上的几种关系,对一个集合${\displaystyle X}$中的${\displaystyle a,b}$和${\displaystyle c}$ 而言,有以下这些关系:
- 自反性:∀a∈S,有a≤a。
- 反对称性:若 $ {\displaystyle a\leq b}$且$ {\displaystyle b\leq a} $ 则 $ {\displaystyle a=b} $。
- 传递性:若${\displaystyle a\leq b} $ 且 $ {\displaystyle b\leq c} $ 则 $ {\displaystyle a\leq c} $。
- 完全性:$ {\displaystyle a\leq b} $ 或 $ {\displaystyle b\leq a} $。
有了这几种关系之后,就可以看看全序和偏序关系分别满足以上的哪些关系了:
- 全序关系:满足反对称性、传递性、完全性。
- 偏序关系:满足反对称性、传递性、自反性。
- 由于完全性也包含自反性,所以全序关系必然也是偏序关系。
可以看到,上面两者的定义差别,仅在自反性和完全性上,完全性要求:集合中任意两个元素都能比较大小,因此:
- 全序:集合中任意两个元素(这两个元素可以相同)在这个关系下都是可以相互比较的。
- 偏序:集合中只有部分元素在这个关系下是可以比较的。
上面的数学定义有些晦涩,我们来举几个直观的例子。
比如整数集合就是一个全序集合,因为任取这个集合中的两个元素,都是能比较其大小的。而一个树形的结构,同一层级的节点之间,由于是同层级的,所以并没有大小之分,从这个意义上来说,这是一种偏序的关系。
再比如,知乎问题全序关系和偏序关系的区别是什么? - 知乎的回答中举了另一个直观的说法:
我来胡说一下,你的家庭关系,就是一个偏序,如果你可以自己到自己的话:
你爷爷生了你爸爸和你叔叔,你爸爸生了你,满足传递;
你不能生你爷爷,满足反对称;
但不是全序,因为你有堂兄弟姐妹(这里认为你叔叔有子女)啊!
那全序是啥?就是九代单传呗
Lamport时钟
了解了物理时间的问题,以及全序、偏序关系的定义,可以正式来到Lamport时钟的解释。
由于物理时钟天然的缺陷,就不能使用这个属性来定义事件的顺序了。Lamport时钟被定义为各进程来维护的一个只能递增的数字(即时间不能发生回退),它有两个规则:
- 规则1:每次进程发出新的事件之前,将本进程当前的Lamport时钟附带在事件上做为事件的一个属性,同时该计数加一。
等一等,前面提到不能使用“物理时钟”是因为各进程的物理时钟不一样,可是规则一中还是使用了各进程维护的一个计数器,这不还是没有解决前面物理时钟遇到的问题吗?于是,进程在接收到事件时还需要遵守规则2:
- 规则2:进程在接收到事件之后,调整接收进程的Lamport时钟为进程当前时钟以及事件中带上的时钟这两者的最大值+1。
用伪代码来表达规则1、2就是:
- 规则1:
# event happens
time = time + 1;
send(message, time);
- 规则2:
(message, incoming_time) = receive();
time = max(incoming_time, time) + 1;
举一个具体的例子:

(引用自Lamport Clock)
上图中:
- 有client、blue、green三个进程组成的分布式系统在工作。
- 在client的时间1,client向blue进程发出了事件,带上了此时client的Lamport时钟1。
- blue在收到client的事件之后,调整本进程的Lamport时钟为 $max(1,收到的事件时间) + 1$
,于是blue进程的时间调整为2。
- 紧跟着blue进程向client进程发出事件,由于上面blue已经调整本地时间为2,于是这个事件的时间为2。
- 其它的可以依次类推,就不再阐述了。
happen-before关系
可以看到,有了上面的两条规则之后,一个分布式系统中的事件,在很多情况(只是很多情况下,并没有全部,下面会展开讨论)下都能定义其先后顺序了,在论文中,lamport将这个关系定义为happen-before关系:
- 引入符号$→ $做为表示事件之间
happen-before的记号。 - 在同一个进程中,如果事件${\displaystyle a}$在事件${\displaystyle b}$之前发生,那么${\displaystyle a → b}$。(这是因为根据规则1,进程每次发出事件之后都会将本地的lamport时钟加一,于是可以在同一个进程内定义事件的先后顺序了)
- 在不同的进程中,如果事件${\displaystyle a}$表示一个进程发出一个事件,事件${\displaystyle b}$表示接收进程收到这个事件,那么也必然满足${\displaystyle a → b}$。(这是因为根据规则2,接收进程在收到事件之后会取本地时钟和事件时钟的最大值并且+1,于是发出事件和接收事件尽管在不同的进程,但是也可以比较其lamport时钟知道其先后顺序了)
- 最后,
happend-before关系是满足传递性的,即:如果${\displaystyle a → b}$且${\displaystyle b → c}$,那么也一定有${\displaystyle a → c}$。
讲到了这里,似乎已经明白了lamport时钟要解决的问题,以及分布式系统中事件之间happend-before关系的定义。但是还有疑点没有解开:
- 一个分布式系统中的事件是否都满足
happen-before关系?按照前面全序、偏序关系的定义,这个问题相当于问:happen-before关系是全序还是偏序关系?
这两个问题可以放在一起解答:分布式系统中的所有事件并不都满足happen-before关系,按照前面全序、偏序关系的定义,由于这个集合中并不是所有情况下都满足这种关系,所以说happen-before关系是一种偏序关系。
以下图来看看:
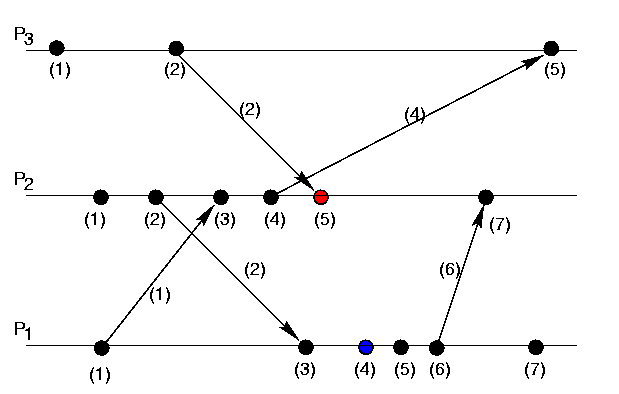
(引用自Lamport Clocks - Kevin Sookocheff)
这个系统的工作方式,在前面解释规则1、2的时候已经有说明,在这里就不再阐述。可以注意到$P_3$进程和$P_2$进程都有一个时间2,在这个时间上这两个进程做了两个不同的事件:
- 从进程$P_3$的视角来看:时间2发出事件给进程$P_2$,按照算法最后进程$P_2$计算出来收到这个事件的时间为5。
- 从进程$P_2$的视角来看,在本进程上时间2也在时间5之前。
所以无论如何,这两个进程上在时间2上发生的事件都不能比较先后顺序了。
如果分布式系统中的两个事件,不满足happen-before关系,在论文中称这两个事件为“并行事件(concurrent event)”。
现实的系统中,确实存在很多并行事件。比如向一个KV系统中同时写入两个并无关联的数据,由于无法根据Lamport时钟对比出先后来,这些操作就可以认为是并行的。
分布式一致性的基础
Lamport时钟本质解决的是如何定义一个分布式系统中不同事件的前后顺序,这是分布式系统一致性的基础。
以日志-状态机模型来看:组成一个分布式系统中的任意一个机器,如果都能按照同一个顺序来“灌入”日志到状态机中,最后都能得到一致的状态。
但是上面在介绍Lamport时钟时,提到过happen-before关系是一种偏序关系,即并不是所有分布式系统中的事件都能有确定的先后顺序,对于这类不能确定先后顺序的事件(如前面提到的$P_3$和$P_2$进程在时间2发生的两件不同事件),可以通过对比其进程ID来确定先后顺序。
综上,如何比较分布式系统中两个事件的先后顺序可以通过下面的算法来完成:
- 如果两个事件满足
happen-before关系,则直接根据这个关系的比较结果返回; - 否则对比发出两个事件的进程ID号。
有了这个补充之后,基于Lamport时钟的分布式事件,就能有一个确定的先后顺序来灌入状态机执行,既然顺序都是一致的最后状态也肯定是一致的:

总结
- 依赖“物理时间”来定义一个分布式系统中事件的先后顺序并不可行。
- 全序、偏序关系的定义:
- 全序:集合中任意两个元素(这两个元素可以相同)在这个关系下都是可以相互比较的。
- 偏序:集合中只有部分元素在这个关系下是可以比较的。
- Lamport时钟的两个更新规则:
- 规则1:每次进程发出新的事件之前,将本进程当前的Lamport时钟附带在事件上做为事件的一个属性,同时该计数加一。
- 规则2:进程在接收到事件之后,调整接收进程的Lamport时钟为当前时钟以及事件中带上的时钟这两者的最大值加一。
- 有了Lamport时钟之后,就能定义一个分布式系统中不同事件之间的
happen-before关系,这种关系是一种偏序关系,不满足happen-before关系的事件,在一个分布式系统中是并行事件。 - Lamport时钟是达成分布式一致性的基础,因为有了这个时钟就能给系统中所有发送的事件定义一个确定的关系。只要系统中的每个状态机都按照一个顺序灌入日志,最终都能达成一致的状态。
回到最初“物理时钟”举的那个例子中,即便采用了Lamport时钟,在物理上看来也可能先后顺序并不同。比如进程A发出的Lamport时钟为1的事件A,以及进程B发出的Lamport时钟为2的事件B,最终在第三者收到的顺序却是相反的:事件B在事件A之前先到达,这是完全有可能的。
换言之,Lamport时钟只是一种逻辑意义上的时间,与物理先后顺序并不一定相同。